Find Parallel Equation Given Point
Parallel and Perpendicular Lines
How to utilize Algebra to detect parallel and perpendicular lines.
Parallel Lines
How do nosotros know when ii lines are parallel?
Their slopes are the same!
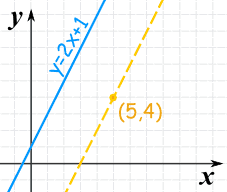
Example:
Find the equation of the line that is:
- parallel to y = 2x + 1
- and passes though the point (5,4)
The slope of y=2x+one is: two
The parallel line needs to accept the same gradient of ii.
We can solve it using the "point-slope" equation of a line:
y − y1 = 2(x − 101)
And so put in the point (5,4):
y − 4 = 2(ten − 5)
And that reply is OK, simply let'due south too put it in y = mx + b course:
y − four = 2x − 10
y = 2x − 6
Vertical Lines
Only this does non work for vertical lines ... I explain why at the end.
Not The Same Line
Be careful! They may be the same line (but with a different equation), and so are non parallel.
How exercise we know if they are really the same line? Check their y-intercepts (where they cross the y-axis) as well every bit their slope:
Example: is y = 3x + 2 parallel to y − 2 = 3x ?
For y = 3x + 2: the slope is three, and y-intercept is two
For y − ii = 3x: the slope is 3, and y-intercept is 2
In fact they are the same line so are not parallel
Perpendicular Lines
Two lines are Perpendicular when they run into at a right angle (90°).
To find a perpendicular slope:
When one line has a slope of m, a perpendicular line has a gradient of −1 grand
In other words the negative reciprocal
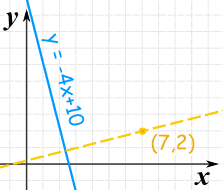
Example:
Find the equation of the line that is
- perpendicular to y = −4x + ten
- and passes though the betoken (7,2)
The slope of y=−4x+ten is: −four
The negative reciprocal of that slope is:
m = −ane −4 = 1 4
So the perpendicular line volition have a slope of 1/4:
y − yi = (1/4)(x − xane)
And now put in the betoken (seven,2):
y − two = (1/iv)(x − 7)
And that answer is OK, just permit'south besides put information technology in "y=mx+b" grade:
y − 2 = x/iv − 7/four
y = ten/four + 1/4
Quick Check of Perpendicular
When we multiply a slope thou past its perpendicular slope −1 m we get simply −one.
And then to quickly check if 2 lines are perpendicular:
When nosotros multiply their slopes, nosotros become −i
Similar this:
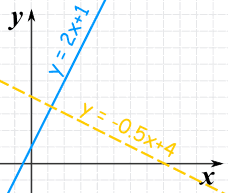
Are these 2 lines perpendicular?
| Line | Slope |
| y = 2x + 1 | 2 |
| y = −0.5x + 4 | −0.five |
When we multiply the two slopes we go:
2 × (−0.v) = −i
Yeah, nosotros got −1, then they are perpendicular.
Vertical Lines
The previous methods work nicely except for a vertical line:
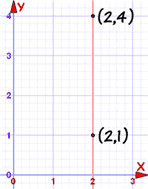
In this case the gradient is undefined (as we cannot divide by 0):
m = yA − yB xA − xB = 4 − one 2 − ii = 3 0 = undefined
So just rely on the fact that:
- a vertical line is parallel to another vertical line.
- a vertical line is perpendicular to a horizontal line (and vice versa).
Summary
- parallel lines: same slope
- perpendicular lines: negative reciprocal slope (−1/m)
Find Parallel Equation Given Point,
Source: https://www.mathsisfun.com/algebra/line-parallel-perpendicular.html
Posted by: gagnonmarkmand.blogspot.com


0 Response to "Find Parallel Equation Given Point"
Post a Comment